EC551 TD2 : Lien entre deux variables

Auteur·rice

Guillaume Franchi

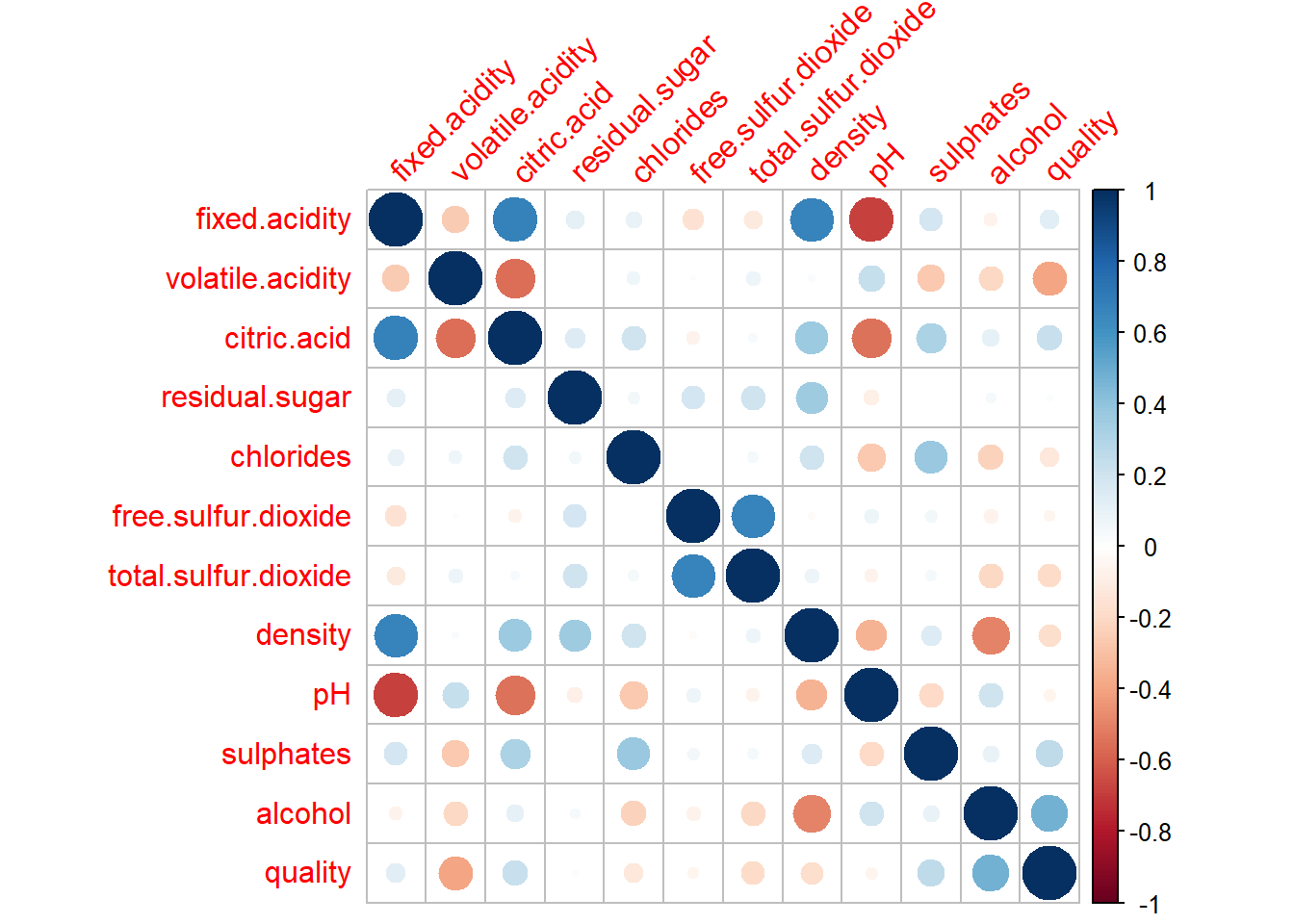
On considère dans ce TD le jeu de données wine.csv, disponible sur connect, donnant des informations sur un échantillon de 1599 vins.

1 Exercice 1 : Lien entre deux variables quantitatives.

  1. Réaliser un résumé statistique de la variable total.sulfur.dioxide.

On s’intéressera aux différents indices de position, de dispersion, et aux outliers. On n’oubliera pas d’effectuer une représentation graphique de ces variables.

  1. A l’aide de la fonction ggpairs()du package GGally, réaliser un nuage de points pour chacun des couples de variables quantitatives du data-frame.

  2. Déterminer la matrice de corrélation de ces variables. Commenter.

  3. A l’aide de la fonction corrplot(), issue du package du même nom, représenter graphiquement cette matrice de corrélation.

Warning: le package 'corrplot' a été compilé avec la version R 4.4.2

2 Exercice 2 : Lien entre une variable quantitative et une variable qualitative.

  1. Créer une variable qualitative cat_alcohol déterminant la catégorie d’alcool de chaque vin. On créera une catégorie par tranche de 1 degré, de 8 à 15 degrés.

2)Résumer cette variable dans un tableau, et la représenter graphiquement :

  • par un diagramme en barres;
  • par un diagramme circulaire.

  1. Créer une fonction VAR() donnant pour un vecteur \(x\) sa variance : \[Var(x) = \dfrac{1}{n} \sum_{i=1}^n (x_i-\overline{x})^2\]

  2. Calculer, pour chaque catégorie d’alcool :

  • La qualité moyenne des vins;
  • La variance de la qualité des vins.
  1. Calculer la variance inter-groupes et la variance intra-groupes de la qualité des vins selon la catégorie d’alcool. Commenter.

3 Lien entre deux variables qualitatives.

  1. Mettre en facteur la variable quality. Résumer cette dernière variable qualitative par un tableau, et la représenter graphiquement.

  2. Dresser la table de contingence des variables quality et cat_alcohol. On pourra utiliser la fonction table().

  3. Calculer la valeur du coefficient \(\chi^2\) d’écart à l’indépendance pour ces deux variables qualitatives. Commenter.

On pourra utiliser la fonction chisq.test() et l’aide de R.